
Avis du pôle scientifique de Kinesport
Pastille verte
Pastille verte
Cette étude longitudinale rétrospective est un article à faible risque de biais, tous les critères méthodologiques majeurs sont respectés permettant de limiter et contrôler au mieux les biais dans l’étude.
De tels modèles sont considérés comme des modèles linéaires à variation temporelle en fonction de la structure de leurs composants et peuvent donc nécessiter un certain nombre d'observations (c'est-à-dire de performances) pour estimer correctement les relations entre la charge d'entraînement et les performances. Pour surmonter certaines de ces limites, des améliorations de l'ancien modèle de réponse impulsionnelle ont été proposés en utilisant un algorithme récursif afin d'estimer les paramètres en fonction de chaque entrée du modèle (c'est-à-dire la charge d'entraînement) et en introduisant des variations de la réponse à la fatigue sur un seul cycle d’entraînement. D'autres adaptations du modèle Fitness-Fatigue ont également été développées dans le but d'améliorer à la fois la qualité de l'ajustement et la précision des prédictions. Néanmoins, les modèles de réponse impulsionnelle ont cherché à atténuer les processus physiologiques sous-jacents impliqués par l'exercice en un petit nombre d'entités pour prédire les effets de l'entraînement tant en endurance (course à pied, vélo, ski et natation) qu’en activités plus complexes (lancer du marteau, gymnastique et judo). Cette approche simpliste pourrait empêcher de saisir la relation appropriée entre l'entraînement et la performance, et finalement nuire à la précision des prédictions. De plus, à l'exception de celui de Matabuena et al., ces modèles supposent que l'effet d'entraînement est maximal à la fin de la séance d'entraînement. Cette hypothèse n'est raisonnable que pour la composante négative du modèle (c'est-à-dire « Fatigue »), où sa valeur maximale est prise immédiatement après la séance. En ce qui concerne les effets positifs induits par l'entraînement (c’est-à-dire « Fitness »), une telle réponse est assez discutable puisque les adaptations physiologiques se poursuivent dès la fin de la séance d'exercice. Par exemple, les adaptations des muscles squelettiques à l'entraînement décrites par l'augmentation de la masse musculaire, la vitesse de raccourcissement des fibres et les modifications de l'activité de la myosine ATPase sont connues pour être progressives plutôt qu'instantanées. Par conséquent, des fonctions sérielles et bi-exponentielles ont été proposées pour contrecarrer ces limitations et mieux décrire les adaptations d'entraînement par des fonctions de croissance et de décroissance exponentielles, en fonction des réponses physiologiques chez le rat.
Une approche plus statistique a été utilisée pour étudier les effets de la charge d'entraînement sur la performance en utilisant une analyse en composantes principales et des modèles mixtes linéaires sur différentes périodes. Ces modèles déduisent des paramètres à partir de toutes les données disponibles (c'est-à-dire en combinant des sujets au lieu d'un modèle par sujet) mais permettent aux paramètres de varier en fonction de l'hétérogénéité entre les athlètes. Le modèle étant multivarié, le caractère multidimensionnel de la performance pourrait être conservé en incluant des informations psychologiques, nutritionnelles et techniques comme prédicteurs. Cependant, les auteurs n'ont pas pris en compte la facette cumulative des charges d'entraînement quotidiennes, où les fonctions cumulatives exponentielles et décroissantes telles que proposées par Candau et al. peuvent convenir à la modélisation des performances.
Des alternatives issues du domaine des sciences informatiques ont également été utilisées pour clarifier la relation charge d'entraînement - performance dans un but prédictif. Plus particulièrement, les approches d'apprentissage automatique sont généralement axées sur la généralisation des modèles (c'est-à-dire la précision avec laquelle un modèle est capable de prédire les valeurs des résultats pour des données inédites). Diverses approches tendent à maximiser un tel critère. Par exemple, on peut effectuer des procédures de validation croisée (cross-validation - CV), dans lesquelles les données sont séparées en ensembles d'apprentissage pour l'estimation des paramètres et en ensembles de tests pour la prédiction. Une telle procédure favorise la détermination de modèles optimaux, par rapport à la famille de modèles considérés et quant à leur capacité de généralisation. Dans le même temps, les procédures de CV permettent de diagnostiquer le sous-ajustement et le sur-ajustement du modèle. Le sous-ajustement décrit généralement un modèle inflexible incapable de capturer des régularités notables dans un ensemble d'observations typiques. En revanche, le surajustement représente un modèle surentraîné, qui a tendance à mémoriser chaque observation particulière, entraînant ainsi des taux d'erreur élevés lors de la prédiction sur des données inconnues. Alors que les études susmentionnées visaient à décrire les relations entre la charge d'entraînement et les performances en estimant les paramètres du modèle et en testant le modèle sur un seul ensemble de données, la généralisation des modèles ne peut être garantie. Cela remet en cause leur utilité dans une application prédictive. D'autre part, les méthodologies de modélisation utilisant des procédures de CV sont la norme dans un but prédictif plutôt que d'être uniquement descriptives. À la connaissance des auteurs, seules quelques études récentes ont modélisé les performances avec des modèles Fitness-Fatigue utilisant une procédure de CV, et l’une d’entre elles a séparé les données en deux ensembles égaux de données d'entraînements et de tests respectivement. Ludwig et al. ont rapporté que l'optimisation de tous les paramètres, y compris le terme de décalage, rend le modèle sujet au surajustement. Par conséquent, les interprétations tirées des prévisions ainsi que des paramètres du modèle peuvent être incorrectes.
Les adaptations physiologiques impliquées par l'exercice étant complexes, certains auteurs ont étudié la relation entre l'entraînement et la performance en utilisant des réseaux neuronaux artificiels (Artificial Neural Networks - ANN), des modèles non linéaires d'apprentissage automatique. Malgré les faibles erreurs de prédiction rapportées (par exemple, une erreur de 0,05 seconde sur une performance de 200m en natation), les considérations méthodologiques de leur étude (principalement influencées par une petite taille d'échantillon) et la nature « boite noire / black-box » des ANN, remettent en question leur utilisation dans la modélisation des performances sportives. Les sciences informatiques offrent de nombreux modèles d'apprentissage automatique, bien qu'elles soient souvent réduites dans les ANN à la prédiction des performances sportives. Si l’on considère les performances sportives, des algorithmes puissants issus de l'apprentissage supervisé pourraient également être envisagés pour résoudre les problèmes de modélisation des performances sportives, soit par une régression, soit par une formulation de classification du problème. Pour n'en citer que quelques-unes, les approches non linéaires telles que les modèles Random Forest (RF) tiennent compte des relations non linéaires entre une cible et un large ensemble de prédicteurs pour faire des prédictions. D'une manière différente, les modèles linéaires tels que les régressions linéaires régularisées ont également prouvé leur efficacité dans des contextes de haute dimensionnalité et de multicolinéarité. Sur cette base, les deux pourraient être utiles à des fins de modélisation des performances sportives.
À ce jour, aucune famille de modèles (c'est-à-dire les modèles de réponse impulsionnelle, basés sur la physiologie, statistiques et d'apprentissage automatique) ne semble être privilégiée pour la prédiction de la performance sportive à partir d’un ensemble de données, principalement en raison d'un manque de preuves et de confiance dans la modélisation des effets de l’entraînement et la précision des prédictions de performance. De plus, comme la capacité de généralisation n'est pas systématiquement évaluée, les interprétations pratiques et physiologiques tirées de certains modèles peuvent être incorrectes et doivent être prises avec prudence.
Afin d'élucider les relations entre les charges d'entraînement et les performances sportives dans une application prédictive, les auteurs ont émis l'hypothèse qu’après une sélection de modèles, des méthodes de régularisation et de réduction de dimension conduiraient à une plus grande capacité de généralisation du modèle que les anciens modèles de réponse impulsionnelle.
Afin de prescrire une programmation d'entraînement optimale, les professionnels du sport ont besoin de comprendre les effets physiologiques impliqués par chaque séance d'entraînement et ses conséquences sur la performance sportive. Ainsi, cette étude visait à fournir une méthodologie robuste et transférable reposant sur la généralisation de modèles dans un contexte de modélisation de la performance sportive. Les auteurs ont collecté des données auprès de patineurs de vitesse sur piste courte de haut niveau, faisant partie de l'équipe nationale française. À ce jour, seules quelques études ont étudié les relations entre l'entraînement et les performances dans ce sport. À partir d'approches de modélisation linéaire et non linéaire, Knobbe et al. ont fourni une méthodologie intéressante autour des méthodes d'agrégation pour fournir des fonctionnalités clés et exploitables des composants d’entraînement. Les auteurs ont étudié des modèles individuels qui représentent des adaptations à l'entraînement et qui pourraient fournir des informations utiles aux entraîneurs impliqués dans des tâches de programmation d'entraînement. Dans un autre ordre d'idées, Méline et al. ont examiné la relation dose-réponse entre l'entraînement et la performance à travers des simulations de surcharge et quelques stratégies de réduction progressive. Le modèle dose-réponse de Busso est apparu comme un modèle précieux pour évaluer les stratégies de réduction progressive et leurs effets potentiels sur les performances de patinage. Cependant, une contribution principalement basée sur le principe de généralisation du modèle semble intéressante en renforçant les connaissances sur la modélisation de la performance sportive dans les sports de haut niveau.
Après avoir construit un ensemble de données approprié, les auteurs ont considéré le modèle variable dose-réponse (DR) comme un schéma de régression de base et l'ont comparé à trois modèles : une régression en composantes principales (principal component regression - PCR), une régression régularisée par un réseau élastique (Elastic net - ENET) et un modèle de régression Random Forest (RF).
Ces modèles permettent de :
Une approche plus statistique a été utilisée pour étudier les effets de la charge d'entraînement sur la performance en utilisant une analyse en composantes principales et des modèles mixtes linéaires sur différentes périodes. Ces modèles déduisent des paramètres à partir de toutes les données disponibles (c'est-à-dire en combinant des sujets au lieu d'un modèle par sujet) mais permettent aux paramètres de varier en fonction de l'hétérogénéité entre les athlètes. Le modèle étant multivarié, le caractère multidimensionnel de la performance pourrait être conservé en incluant des informations psychologiques, nutritionnelles et techniques comme prédicteurs. Cependant, les auteurs n'ont pas pris en compte la facette cumulative des charges d'entraînement quotidiennes, où les fonctions cumulatives exponentielles et décroissantes telles que proposées par Candau et al. peuvent convenir à la modélisation des performances.
Des alternatives issues du domaine des sciences informatiques ont également été utilisées pour clarifier la relation charge d'entraînement - performance dans un but prédictif. Plus particulièrement, les approches d'apprentissage automatique sont généralement axées sur la généralisation des modèles (c'est-à-dire la précision avec laquelle un modèle est capable de prédire les valeurs des résultats pour des données inédites). Diverses approches tendent à maximiser un tel critère. Par exemple, on peut effectuer des procédures de validation croisée (cross-validation - CV), dans lesquelles les données sont séparées en ensembles d'apprentissage pour l'estimation des paramètres et en ensembles de tests pour la prédiction. Une telle procédure favorise la détermination de modèles optimaux, par rapport à la famille de modèles considérés et quant à leur capacité de généralisation. Dans le même temps, les procédures de CV permettent de diagnostiquer le sous-ajustement et le sur-ajustement du modèle. Le sous-ajustement décrit généralement un modèle inflexible incapable de capturer des régularités notables dans un ensemble d'observations typiques. En revanche, le surajustement représente un modèle surentraîné, qui a tendance à mémoriser chaque observation particulière, entraînant ainsi des taux d'erreur élevés lors de la prédiction sur des données inconnues. Alors que les études susmentionnées visaient à décrire les relations entre la charge d'entraînement et les performances en estimant les paramètres du modèle et en testant le modèle sur un seul ensemble de données, la généralisation des modèles ne peut être garantie. Cela remet en cause leur utilité dans une application prédictive. D'autre part, les méthodologies de modélisation utilisant des procédures de CV sont la norme dans un but prédictif plutôt que d'être uniquement descriptives. À la connaissance des auteurs, seules quelques études récentes ont modélisé les performances avec des modèles Fitness-Fatigue utilisant une procédure de CV, et l’une d’entre elles a séparé les données en deux ensembles égaux de données d'entraînements et de tests respectivement. Ludwig et al. ont rapporté que l'optimisation de tous les paramètres, y compris le terme de décalage, rend le modèle sujet au surajustement. Par conséquent, les interprétations tirées des prévisions ainsi que des paramètres du modèle peuvent être incorrectes.
Les adaptations physiologiques impliquées par l'exercice étant complexes, certains auteurs ont étudié la relation entre l'entraînement et la performance en utilisant des réseaux neuronaux artificiels (Artificial Neural Networks - ANN), des modèles non linéaires d'apprentissage automatique. Malgré les faibles erreurs de prédiction rapportées (par exemple, une erreur de 0,05 seconde sur une performance de 200m en natation), les considérations méthodologiques de leur étude (principalement influencées par une petite taille d'échantillon) et la nature « boite noire / black-box » des ANN, remettent en question leur utilisation dans la modélisation des performances sportives. Les sciences informatiques offrent de nombreux modèles d'apprentissage automatique, bien qu'elles soient souvent réduites dans les ANN à la prédiction des performances sportives. Si l’on considère les performances sportives, des algorithmes puissants issus de l'apprentissage supervisé pourraient également être envisagés pour résoudre les problèmes de modélisation des performances sportives, soit par une régression, soit par une formulation de classification du problème. Pour n'en citer que quelques-unes, les approches non linéaires telles que les modèles Random Forest (RF) tiennent compte des relations non linéaires entre une cible et un large ensemble de prédicteurs pour faire des prédictions. D'une manière différente, les modèles linéaires tels que les régressions linéaires régularisées ont également prouvé leur efficacité dans des contextes de haute dimensionnalité et de multicolinéarité. Sur cette base, les deux pourraient être utiles à des fins de modélisation des performances sportives.
À ce jour, aucune famille de modèles (c'est-à-dire les modèles de réponse impulsionnelle, basés sur la physiologie, statistiques et d'apprentissage automatique) ne semble être privilégiée pour la prédiction de la performance sportive à partir d’un ensemble de données, principalement en raison d'un manque de preuves et de confiance dans la modélisation des effets de l’entraînement et la précision des prédictions de performance. De plus, comme la capacité de généralisation n'est pas systématiquement évaluée, les interprétations pratiques et physiologiques tirées de certains modèles peuvent être incorrectes et doivent être prises avec prudence.
Afin d'élucider les relations entre les charges d'entraînement et les performances sportives dans une application prédictive, les auteurs ont émis l'hypothèse qu’après une sélection de modèles, des méthodes de régularisation et de réduction de dimension conduiraient à une plus grande capacité de généralisation du modèle que les anciens modèles de réponse impulsionnelle.
Afin de prescrire une programmation d'entraînement optimale, les professionnels du sport ont besoin de comprendre les effets physiologiques impliqués par chaque séance d'entraînement et ses conséquences sur la performance sportive. Ainsi, cette étude visait à fournir une méthodologie robuste et transférable reposant sur la généralisation de modèles dans un contexte de modélisation de la performance sportive. Les auteurs ont collecté des données auprès de patineurs de vitesse sur piste courte de haut niveau, faisant partie de l'équipe nationale française. À ce jour, seules quelques études ont étudié les relations entre l'entraînement et les performances dans ce sport. À partir d'approches de modélisation linéaire et non linéaire, Knobbe et al. ont fourni une méthodologie intéressante autour des méthodes d'agrégation pour fournir des fonctionnalités clés et exploitables des composants d’entraînement. Les auteurs ont étudié des modèles individuels qui représentent des adaptations à l'entraînement et qui pourraient fournir des informations utiles aux entraîneurs impliqués dans des tâches de programmation d'entraînement. Dans un autre ordre d'idées, Méline et al. ont examiné la relation dose-réponse entre l'entraînement et la performance à travers des simulations de surcharge et quelques stratégies de réduction progressive. Le modèle dose-réponse de Busso est apparu comme un modèle précieux pour évaluer les stratégies de réduction progressive et leurs effets potentiels sur les performances de patinage. Cependant, une contribution principalement basée sur le principe de généralisation du modèle semble intéressante en renforçant les connaissances sur la modélisation de la performance sportive dans les sports de haut niveau.
Après avoir construit un ensemble de données approprié, les auteurs ont considéré le modèle variable dose-réponse (DR) comme un schéma de régression de base et l'ont comparé à trois modèles : une régression en composantes principales (principal component regression - PCR), une régression régularisée par un réseau élastique (Elastic net - ENET) et un modèle de régression Random Forest (RF).
Ces modèles permettent de :
- Présenter et discuter de l’utilité des méthodes de régularisation et de réduction de dimension par rapport au concept de généralisation.
- Modéliser les performances sportives à l'aide de modèles robustes à haute dimensionnalité et multicolinéarité et étudier les facteurs clés de la performance en patinage de vitesse sur piste courte.
Méthodes
Il s’agit d’une étude longitudinale rétrospective
Participants
-
Age moyen 22,7 ± 3,4 ans
-
3 hommes (masse corporelle de 71,4 ± 9,4 kg)
-
4 femmes (masse corporelle de 55,9 ± 3,9 kg)
Chaque athlète a vécu les Jeux Olympiques d'Hiver 2018 de PyeongChang, en Corée du Sud (n = 2) ou préparait les Jeux olympiques de Pékin, en Chine (n = 7).
Les données ont été recueillies au cours d'une période d'entraînement de trois mois sans compétition, interrompue par une pause de deux semaines et débutant un mois après la reprise de l'entraînement pour une nouvelle saison.
La présente étude rétrospective s'est appuyée sur les données collectées sans provoquer de changements dans la programmation de l'entraînement des athlètes.
Toute l'équipe était entraînée par le même entraîneur, responsable de la programmation des entraînements et de la collecte des données. Le volume hebdomadaire moyen d'entraînement était de 16,6 ± 2,5 heures.
Les données ont été recueillies au cours d'une période d'entraînement de trois mois sans compétition, interrompue par une pause de deux semaines et débutant un mois après la reprise de l'entraînement pour une nouvelle saison.
La présente étude rétrospective s'est appuyée sur les données collectées sans provoquer de changements dans la programmation de l'entraînement des athlètes.
Ensemble de données
Variable dépendante : la performance
Les participants ont effectué chaque semaine des contre-la-montre en départ debout (distance = 166,68 mètres, soit 1,5 tour) après un échauffement standardisé.
248 performances ont été enregistrées pour une moyenne de 35,4±2,23 performances individuelles.
Le test de performance étant un gold standard pour l'évaluation de la capacité d'accélération, les athlètes étaient tous familiarisés avec ce test avant l'étude.
Résumé des variables indépendantes
Variables indépendantes
Xi
Description
Agrégation
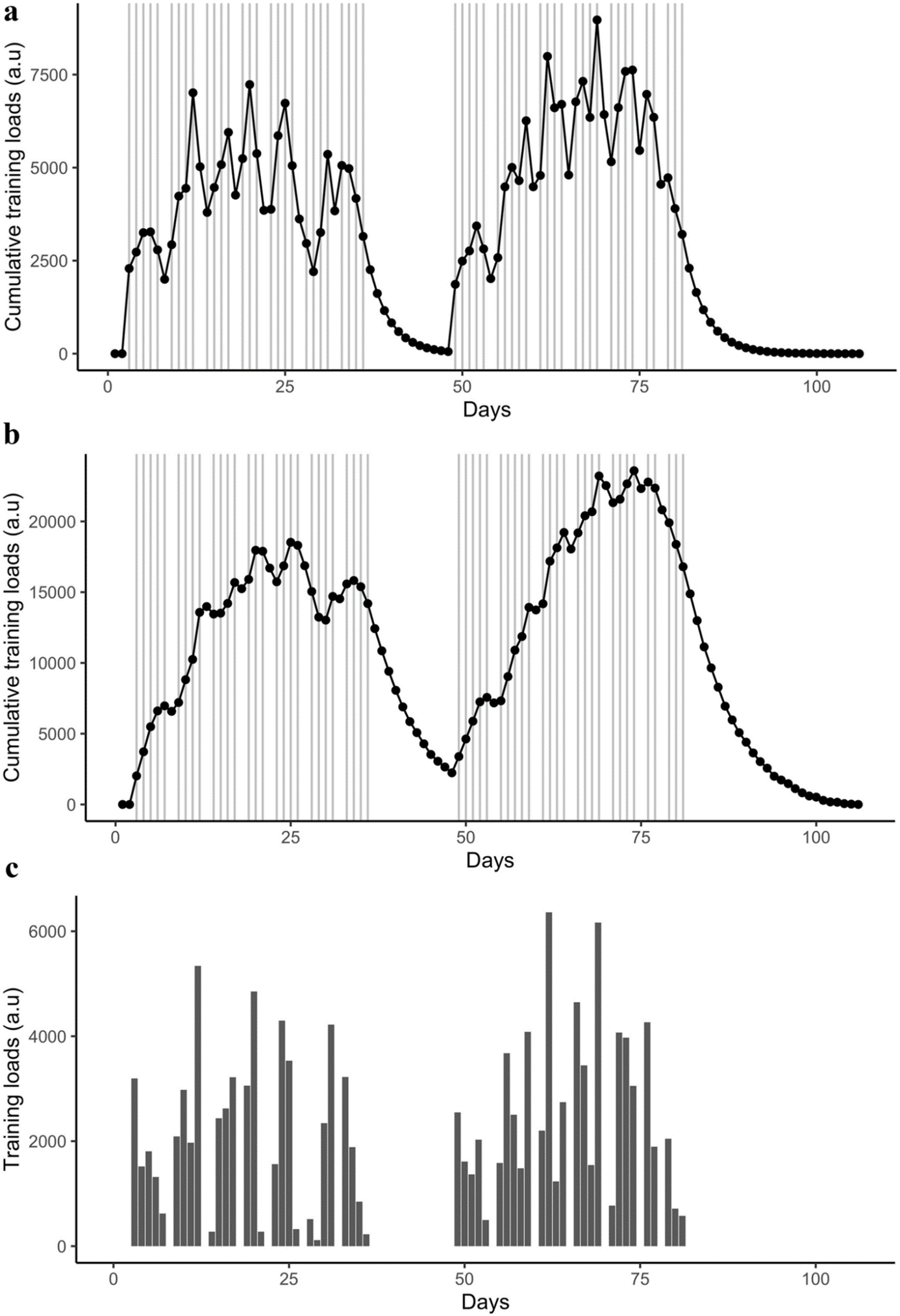
Charges d'entraînement quotidiennes cumulées d'un athlète représentatif suivant (a) la fonction de réponse impulsionnelle et la fonction de réponse bi-exponentielle en série. (c) illustre les charges d'entraînement quotidiennes brutes X1, exprimées par w(t). Dans (a) et (b), les points représentent les valeurs quotidiennes de la charge d'entraînement cumulée et les lignes pleines verticales indiquent l'occurrence des sessions d'entraînement. Les valeurs sont représentées en unités arbitraires (a.u).
Résultats
Grace à la validation croisée des séries temporelles, les modèles ont fourni une généralisation et une prédiction de performance hétérogènes. Les distributions des erreurs quadriatiques moyennes par modèle sont illustrées ici :
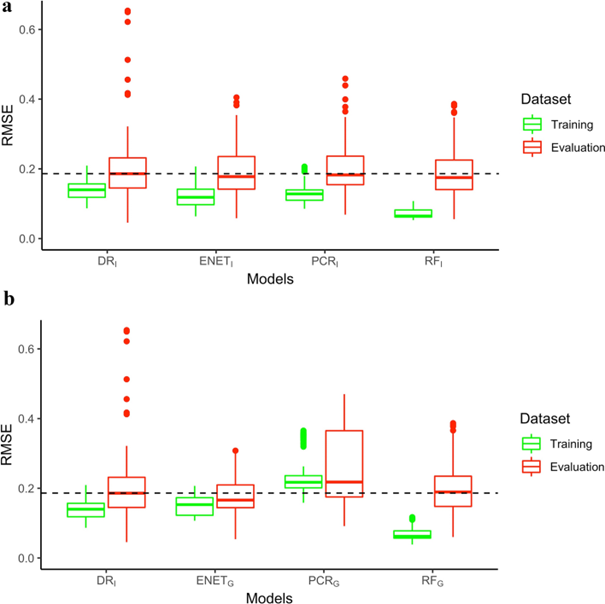
Généralisation des modèles
L'analyse des modèles mixtes a montré que les modèles ENET et PCR réduisaient les différences en termes d'erreurs de prédiction entre les ensembles de données d’entraînement et d'évaluation.
Les modèles les plus généralisables étaient les modèles ENET et PCR calculés sur des données globales, suivis des modèles basés sur des individus. D'une manière générale, les modèles construits en groupe offraient probablement une plus grande capacité de généralisation que les modèles basés sur des individus.
Prédiction des performances
Les erreurs quadratiques moyennes (RMSE) rapportées sur les données d'évaluation à l'aide d'une analyse de modèle mixte ont indiqué que ENETG était le modèle qui contribuait le plus à réduire les erreurs de prédiction, suivi de RFG. En conséquence, un effet significatif de la classe du modèle sur les erreurs de prédiction a été signalé. Le calcul des modèles sur une plus grande population (c'est-à-dire les modèles basés sur le groupe) n'a montré qu'une tendance en faveur des modèles basés sur le groupe sur le taux de réponse aux erreurs.
Les distributions des RMSE sur les données utilisées pour l'évaluation des modèles ont montré une variance hétérogène entre les modèles. Les écarts types les plus importants ont été constatés pour DRI et PCRG. Les modèles ENET, PCRI et RF ont fourni des performances plus cohérentes avec des écarts types inférieurs compris dans des intervalles de [0,023 ; 0,027] et [0,012 ; 0,017] pour les modèles calculés individuels et de groupe, respectivement.
Les prédictions faites à partir des deux modèles les plus généralisables (ENETG et PCRG), et de la référence DRI illustrent la sensibilité des modèles pour un athlète représentatif :
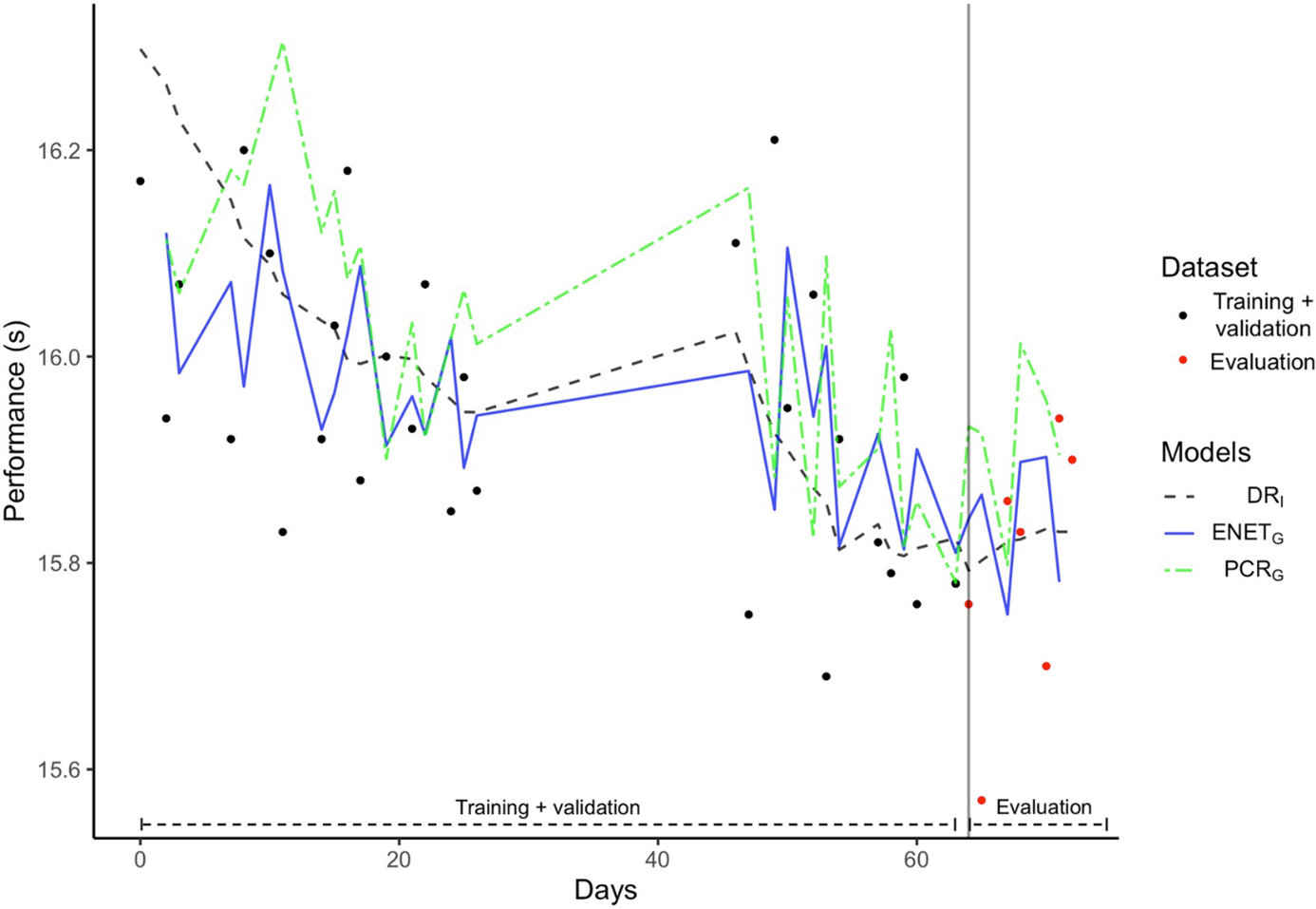
Les performances modélisées à partir du modèle DRI étaient relativement stables et moins sensibles aux variations réelles des performances. L'écart-type calculé sur les données utilisées pour l'évaluation du modèle confirme cette prédiction régulière avec σ=0,015, σ=0,071 et σ=0,062 pour DRi, PCRG et ENETG, respectivement. En ce qui concerne ENETG, les coefficients standardisés les plus élevés ont été attribués à la composante auto-régressive (c'est-à-dire la performance passée), suivie du facteur athlète puis des agrégations impulsionnelles et bi-exponentielles en série. Pour la régression, le PCRG a utilisé les trois premières composantes principales expliquant respectivement 52,3%, 16,5% et 7,6% de la variance totale.
Conclusion
- Cette étude nous fournit une méthodologie de modélisation transférable qui repose sur l'évaluation de la capacité de généralisation des modèles dans un contexte de modélisation de la performance sportive.
- Le modèle mathématique variable dose-réponse avec les modèles Elastic net (ENET), régression en composantes principales (PCR) et Random Forest (RF) ont fait l'objet d'une validation croisée dans un cadre de séries chronologiques.
- La généralisation du modèle DR (dose-réponse) a été surpassée par les modèles ENET et PCR, bien que les résultats ne puissent pas être comparés directement avec la littérature.
- Le modèle ENET a fourni les meilleures performances à la fois en termes de généralisation et de précision de la prédiction des performances par rapport aux modèles DR, PCR et RF.
- Globalement, l'augmentation de la taille de l'échantillon en calculant des modèles sur l'ensemble du groupe d'athlètes a conduit à des modèles plus performants que ceux calculés individuellement.
- Dans cette étude, l'utilisation de méthodes de régularisation et de réduction de la dimension pour traiter les problèmes de haute dimensionnalité et de multicollinéarité a été favorisée. Cependant, d'autres modèles pourraient s'avérer utiles pour la modélisation de la performance athlétique.
- La méthodologie mise en évidence dans cette étude peut être réemployée quelles que soient les données, dans le but d'optimiser les performances du sport d'élite par des simulations de protocoles d'entraînement.
- D'autres recherches impliquant des simulations de séances d'entraînement et des évaluations de modèles dans le domaine de la prévision permettraient de mettre en évidence la pertinence de certaines familles de modèles pour l'optimisation de la programmation de l'entraînement.
L'article
Imbach F, Perrey S, Chailan R, Meline T, Candau R. Training load responses modelling and model generalisation in elite sports. Sci Rep. 2022 Jan 28;12(1):1586. doi: 10.1038/s41598-022-05392-8. PMID: 35091649; PMCID: PMC8799698.



